Enhedsvektor notation | Vektorer og rum | Lineær algebra | Khan Academy
Når de forklarer dimension W, repræsenteres den som den negative side af X-aksen. Hvorfor er dimension W negativ X? Er det ikke virkelig dens egen dimension?

- Prøv at tegne en 4-dimensionel graf på en 2-dimensionel overflade. Dette er hvad de kom på (din ret, selvom det ikke er en fantastisk graf).
Som @NendoTaka har nævnt, er det ret svært at tegne et 4d-objekt på en 2d-overflade.
Sådan fungerer dimensionalitet:
med en enkelt dimension sendes et punkt uendeligt, hvilket skaber en linje (se X)
i 2d tilføjer vi en dimension vinkelret på den (se X, Y).
Derefter går vi vinkelret igen og udvider opad for at få den tredje dimension (Se X, Y, Z).
Fordi 3d> 2d, kan vi ikke repræsentere det godt på papir uden at folde papiret eller tilføje flere ark oven på det - alt sammen virkelig upraktisk til visning på en skærm. Så i stedet bruger vi perspektiv - hvordan vores øjne opfatter 3d. Normalt er vinklerne her ~ 30 grader.

Og det ser ret okay ud, for vores øjne ser ikke i denne traditionelle 3d-forstand, så efterligner det, der fungerer. Men når vi vil repræsentere en 4. dimension, har vi ikke noget at sammenligne det med. Vi er nødt til at gå vinkelret igen, og det er svært for vores øjne at forstå, da vi ikke har meget af en reference.
Her er et eksempel på en 4. dimension:
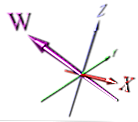
Dette er en mere korrekt måde at vise dimensionen på, men den er stadig afhængig af perspektiv - det er heller ikke umiddelbart indlysende, at det er en ny dimension ved første øjekast.
Animatorerne valgte sandsynligvis at gøre noget simpelt, der ville være lettere at animere. Skønt du roterer ovenstående billede, kan X- og W-dimensionerne overlappe hinanden - og dette ville ikke være indlysende i billedet uden pilemarkører.
Så ja, de tager fejl - men der er heller ikke en enkel måde at repræsentere 4 dimensioner på et enkelt ark papir
Koordiner billedkilder og en god læsning
3- 1 For at være retfærdig er der mange standardmetoder til at projicere 4-dimensionelle objekter som tesserakter og 3-sfærer i 3 dimensioner (og derefter ned til 2 dimensioner på de sædvanlige måder), der er langt bedre end den, der blev brugt i showet, mange hvoraf har den ekstra bonus at se coolere ud end den, der blev brugt i showet.
- @senshin åh helt sikkert, men jeg antager, at animatorerne også ville forklare noget snarere end at forbløffe
- 1 Du kan bruge andre ting end position til at angive, hvor langt langs en akse noget er, som farve.